Dr. Yang is an Assistant Professor in School of Computer Science and Technology / Faculty of Innovation Engineering at Macau University of Science and Technology (M.U.S.T. 澳門科技大學). Before he joined M.U.S.T., he was a postdoctoral researcher at Sun Yat-sen University (2021.12-2023.06). He obtained his doctoral degree in Applied Mathematics, Korea University, 2021 under the guidance of Prof. Junseok Kim. His research interests are Computational Multi-phase Fluid Dynamics, Phase-field Method, Numerical Simulations in Science and Engineering, and Mathematical Modeling. He has published 66 SCI papers as first or corresponding author from 2018.

I only recruit 1-3 Master students in each year. If you are willing to join my team, please contact me via jxyang@must.edu.mo

已主持科研項目如下：

國家自然科學基金青年科學基金項目;

澳門科技大學研究基金項目;

博士後科學基金面上項目。

博士期間被中國駐韓大使館教育處評為2020年度優秀在韓國家公派留學人員; 入選2022年度博士後國際交流計劃引進項目。

Introduction of PF_CFD Team

PF_CFD Team (相場_計算流體動力學 課題組) aims to develop high-performance mathematical models and computational algorithms in science and engineering. As a leader of my lab, I have published more than 90 SCI papers from 2018 and accumulated related experiences and skills in the fileds of phase-field method and incompressible fluid simulations. Moreover, I am also interested in immersed boundary method, level-set method, lattice Boltzmann method, image processing, 3D volume reconstruction, and digital twins.

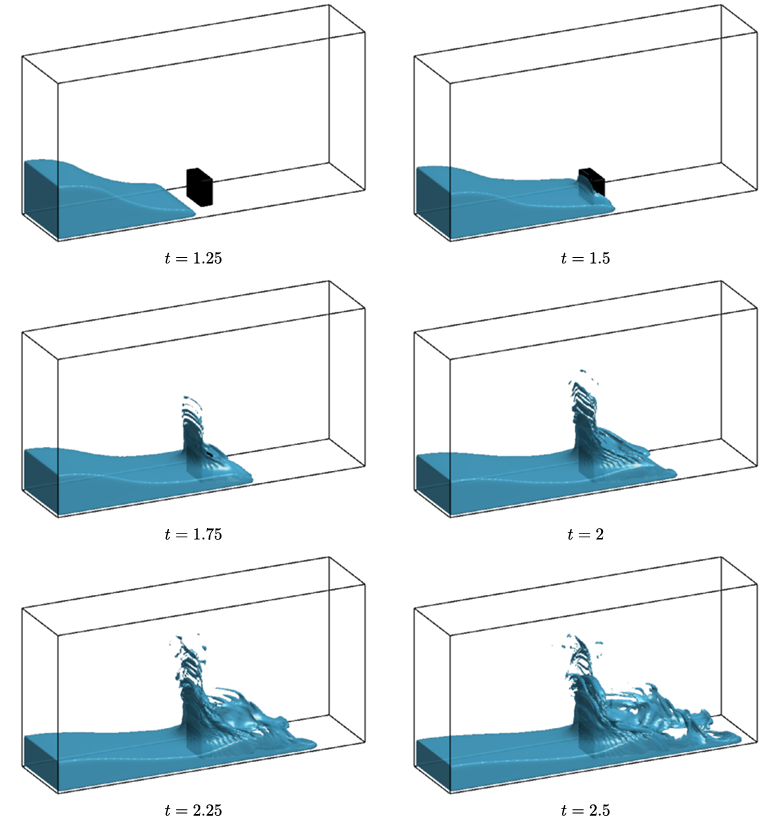
In my homepage, I provide several simple but practical MATLAB codes for interested readers or students. These codes can be used to simulate phase-field Cahn-Hilliard dynamics, Fluid flows, square phase-field crystal dynamics, dendritic growth, Natural convection, and Image segmentation, etc. I will update other open source codes in the future. In the Publications, I only provide the papers as first or corresponding author. For more details of my publications, please refer to my ResearchGate page. Some interesting simulation results are pasted in Portfolio.

Present research topics (selected)

• Computational Fluid Algorithms:
  1. Structure-preserving time-marching schemes for the incompressible Navier-Stokes equations;
  2. Finite volume method for the fluid flows on surfaces with direct discretization;
  3. Finite volume lattice Boltzmann algorithms for fluid flows on curved surfaces;
  4. Closest point-type finite difference method for the Navier-Stokes equations on surfaces;
  5. Efficient and high-order accurate algorithms for fluid-structure interactions.
• Numerical Simulations of Multi-phase Fluids:
  1. Strongly stable numerical methods for two-phase flows with large desnity ratio and high Reynolds number;
  2. Energy-stable and linear schemes for multi-phase flows with variable density and viscosity;
  3. Accurate, stable, and efficient algorithms for multi-phase fluids in complex domains;
  4. Multi-physics coupled fluid modeling and the associated numerical computations;
  5. Hybrid phase-field / lattice Boltzmann / immersed boundary methods in complex fluid simulations.
• Computational Biology and Material Sciences:
  1. Phase-field modeling of red blood cell and its structure-preserving algorithms;
  2. Immersed boundary-diffuse interface method for simulating cell division;
  3. Mathematical modeling of tumor growth and tissue growth;
  4. Accurate and highly efficient algorithms for crystal and quasi-crystal models;
  5. Energy-stable computations for copolymers in irregular regions.
• Image Processing and Volume Reconstruction:
  1. Maximum principle-preserving numerical methods for phase-field models of image segmentation;
  2. Unconditionally stable numerical methods for phase-field models of 3D volume reconstruction;
  3. Lattice Boltzmann-Threshold dynamics methods for image processing.
• Numerical Methods for Partial Differential Equations:
  1. Error estimations of convex splitting-type methods for the Swift-Hohenberg equations;
  2. Adaptive narrow band algorithms for solving Allen-Cahn and Cahn-Hilliard equations;
  3. Novel explicit and practically stable methods for gradient flow problems;
  4. Multigrid algorithms for accelerating the convergence.

Open positions / 招生信息

Master degree in Applied Mathematics openings on computational physics (fluids, biology, and materials) and numerical methods for partial differential equations (PDEs). Undergraduate students should contact Prof. Yang and apply to School of Computer Science and Engineering at Macau University of Science and Technology.

For the students who want to study numerical simulations with me, the prerequisites are: Calculus (Advanced Mathematics), Linear Algebra, and College Physics. Mastering C program, MATLAB, Latex and passing a numerical analysis course are recommended.

欢迎具有數學、工程力學、物理等相關本科背景的同學報考碩士課程！個人精力有限，每年只招收碩士1-3名，暫無法招收博士，若有意向，請提前通過郵件 jxyang@must.edu.mo 聯繫我，謝謝關注！